轨道基本知识学习(1)
本章重点记录轨道六根数、轨道六根数转位置速度矢量、轨道运行公式 知识点。
本章重点记录轨道六根数、轨道六根数转位置速度矢量、轨道运行公式知识点
轨道六根数(orbital elements)
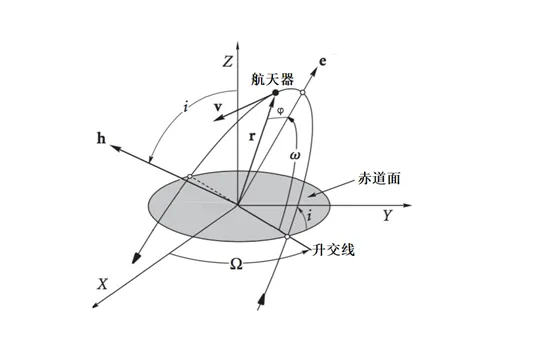
在二体问题中,轨道根数(orbital elements)是描述物体运动轨迹的简便形式。三维空间中,唯一确定物体轨迹需要六个参数,如位置矢量和速度矢量(均为三维)可共同确定物体轨迹。此外,用六个轨道根数也可描述它。通常的轨道六根数指的是:半长轴a、离心率e、轨道倾角i、近心点辐角ω、升交点经度Ω和真近点角φ。经过三角函数运算,它们能表示出物体所处特定位置和速度。
半长轴 (a):轨道的大小和周期。
离心率 (e):描述轨道偏离圆形的程度。
轨道倾角 (i):轨道平面与地球赤道平面的夹角。
近心点辐角 (ω):轨道上近心点的角度。 (近心点,轨道离地心最近的点) 升交点经度 (Ω):轨道上升交点的经度。 (升交线,轨道平面与xy平面切线)
真近点角 (φ):卫星在轨道上的位置角度。
z 轴:垂直于轨道平面的法线方向(由右手定则确定,与轨道角动量方向一致)。 x 轴:指向春分点(vernal equinox)。 y 轴:与 x 轴、z 轴构成右手直角坐标系(y = z × x)。
常用公式
轨道的本质
轨道是航天器在引力场的作用下,绕行中心天体按特定规律运动所形成的路径。开普勒第一定律表示,行星的轨道都是一个以恒星为焦点之一的椭圆。
椭圆具有两个焦点,在太阳系中,太阳就位于行星椭圆轨道的其中一个焦点上。以太阳为中心的极坐标系统用于描述行星相对于太阳的运动关系,在数学上,椭圆可以用公式表示: \(\begin{equation} r=\frac{a(1-e^2)}{1+ecos\theta} \end{equation}\)
其中,r为航天器到中心天体的距离,a为轨道半长轴,e为偏心率,θ为真近点角。
地球同步轨道(GEO):地球同步轨道的高度约为35786公里,轨道周期与地球自转周期相同,使得卫星在该轨道上相对于地球保持静止。
轨道运行公式
轨道与运动状态:轨道的形状和位置不仅由初始条件决定,还与航天器的速度和加速度密切相关。根据开普勒第二定律,航天器在轨道上运动时,与中心天体连线在单位时间内扫过的面积保持恒定,这意味着航天器在近地点运动较快,远地点运动较慢。运动状态的变化可以通过以下微分方程描述:
\[\begin{equation} \frac{d^2\overrightarrow{r}}{d\overrightarrow{t}^2}=-\frac{GM}{r^3}\overrightarrow{r} \end{equation}\]其中,G为引力常数,M为中心天体的质量,$\overrightarrow{r}$ 为位置向量。
开普勒第三定律
根据开普勒第三定律,轨道周期T与半长轴a的关系为: \(\begin{equation} T^2=\frac{4\pi^2a^3}{GM} \end{equation}\)
偏心率$e$
偏心率描述轨道的离心程度,0≤e<1表示椭圆轨道,e=0为圆轨道。偏心率越大,轨道越扁长,影响航天器在轨道上的速度分布和能量需求。偏心率的表达式为: \(\begin{equation} e=\sqrt{1-\frac{b^2}{a^2}} \end{equation}\)
其中,b为轨道的半短轴。
轨道六根数转位置速度矢量
轨道坐标系经过三次方向余弦矩阵变换即可变为中心天体惯性系。ECI(地心惯性坐标系) \(\begin{equation} r_{ECI}=\widehat{r}=Rr_p \end{equation}\) \(\begin{equation} r=\frac{1-e^2}{1+ecosφ} \end{equation}\) 旋转顺序:升交点经度Ω -> 轨道倾角i -> 近心点辐角ω
\[\begin{equation} \widehat{r}=[R_3(Ω)R_1(i)R_3(w)]^T \begin{bmatrix} rcosφ\\ rsinφ\\ 0\\ \end{bmatrix} \end{equation}\] \[\begin{equation} R_3(Ω)=\begin{bmatrix} cosΩ&sinΩ&0\\ -sinΩ&cosΩ&0\\ 0&0&1\\ \end{bmatrix}R1(i) \end{equation}\] \[R_1(i)=\begin{bmatrix} 1&0&0\\ 0&cosi&sini\\ 0&-sini&cosi\\ \end{bmatrix}R1(i)\] \[R_3(w)=\begin{bmatrix} cosw&sinw&0\\ -sinw&cosw&0\\ 0&0&1\\ \end{bmatrix}\]